Agol’s Virtual Haken Theorem (part 1)

I am in Paris attending a workshop at the IHP where Ian Agol has just given the first of three talks outlining his proof of the Virtual Haken Conjecture and Virtual Fibration Conjecture in 3-manifold topology (hat tip to Henry Wilton at the Low Dimensional Topology blog from whom I first learned about Ian’s announcement last week). I think it is no under overstatement to say that this marks the end of an era in 3-manifold topology, since the proof ties up just about every loose end left over on the list of problems in 3-manifold topology from Thurston’s famous Bulletin article (with the exception of problem 23 — to show that volumes of closed hyperbolic 3-manifolds are not rationally related — which is very close to some famous open problems in number theory). The purpose of this blog post is to say what the Virtual Haken Conjecture is, and some of the background that goes into Ian’s argument. I hope to follow this up with more details in another post (after Agol gives talks 2 and 3 this coming Wednesday). Needless to say this post has been written in a bit of a hurry, and I have probably messed up some crucial details; but if that caveat is not enough to dissuade you, then read on.

We make the assumption in what follows that all manifolds under discussion are smooth (this is not a problem in 3-manifold topology, where the categories TOP, PL and DIFF are all equivalent) and orientable (which can be achieved by passing to double covers, if necessary).

A compact 3-manifold M, possibly with boundary, is said to be irreducible if every embedded 2-sphere in M bounds a 3-ball in M. A compact 3-manifold is said to be Haken (the terminology sufficiently large is also standard) if it is irreducible, and if it contains a closed, 2-sided properly embedded surface S (other than a 2-sphere) which is incompressible and boundary incompressible; incompressibility means that if an embedded disk intersects S only in an embedded loop, then this loop is (homotopically) inessential in S, and boundary incompressibility means that if an embedded disk intersects S only in a proper arc (with the rest of the boundary of the disk on the boundary of M) then the arc on S is (homotopically) inessential in S. Incompressibility and boundary incompressibility mean roughly that the surface can’t be simplified by a “local” move. Such a surface is also said to be essential. Wolfgang Haken used such surfaces to solve the homeomorphism problem for the 3-manifolds that contain them. This includes as a very important special case manifolds obtained as complements of (open tubular neighborhoods of) knots in the 3-sphere; hence Haken’s methods solve the knot recognition problem — the problem of deciding when two different diagrams determine the same knot type. The key point of Haken’s approach is that once one has an essential surface, one can cut along it to produce a simpler 3-manifold with boundary.  Every irreducible 3-manifold with nonempty boundary is Haken, so if this decomposition process can be begun, it can be continued. (One way to see this is to observe that every nontrivial relative 2-dimensional homology class in a 3-manifold contains an essential surface. Now, 2-dimensional relative homology is dual to 1-dimensional absolute (co-)homology in a 3-manifold. Moreover, exactly half the rank of 1-dimensional (co-)homology of the boundary of a 3-manifold is killed under the inclusion; hence an irreducible 3-manifold with boundary — other than the 3-ball — has nontrivial relative 2-dimensional homology and is therefore Haken). After decomposing along finitely many such pieces, one obtains at the end a finite collection of 3-balls; turning this procedure upside down, a Haken 3-manifold is one that can be obtained from 3-balls by gluing in certain special controlled ways. This opens the possibility of inductive proofs of theorems about Haken 3-manifolds; Thurston’s famous geometrization theorem for Haken 3-manifolds is such an example. The Virtual Haken Conjecture, formulated by Waldhausen in 1968, says that every aspherical (i.e. with trivial for ) closed 3-manifold has a finite cover which is Haken.

Among the most beautiful and interesting examples of Haken 3-manifolds are those that fiber over the circle. These are obtained by taking a surface S (usually assumed by convention to have non-positive Euler characteristic) and a self homeomorphism and forming the mapping torus . The fibers are the slices ; these are all essential, so 3-manifolds that fiber over the circle are Haken. Thurston’s Virtual Fibration Conjecture says that every hyperbolic 3-manifold M has a finite cover which fibers over the circle. Since the “generic” closed 3-manifold (in a suitable sense) is now known to be hyperbolic (by Perelman), this says that essentially all aspherical irreducible 3-manifolds — with some very well-understood simple exceptions — are virtually fibered. Ian already showed that Haken hyperbolic 3-manifolds whose fundamental group satisfies a certain technical condition (called “RFRS”, or “reefers”) satisfy the VFC. Wise’s work shows that Haken 3-manifolds have fundamental group satisfying this condition, so Ian’s work proves the VFC too.

There are many other amazing corollaries of Ian’s theorem, including the fact that the fundamental group of every hyperbolic 3-manifold has a finite index subgroup which surjects onto a free group of rank 2 (i.e. it is “large”), has a finite index subgroup which is bi-orderable, injects in for some , and so on. It is hard to think of a question about fundamental groups of hyperbolic 3-manifolds that it doesn’t answer.

Ian’s preprint is only 31 pages long (although some of it is quite dense), but it rests on a considerable amount of prior work by many people (including Ian himself), of which the biggest breakthrough is of course Perelman’s proof of the geometrization theorem (see here, here and here). Other substantial pieces of the puzzle are the Kahn-Markovic proof of the surface subgroup conjecture, and Wise’s work on special cube complexes. In fact, the technical content of Ian’s preprint is the proof of a conjecture in Wise’s paper about groups acting on CAT(0) cube complexes. So let’s start with the definition of a CAT(0) cube complex.

Definition: A cube complex is a space obtained by gluing Euclidean cubes of edge length 1 along subcubes. It is CAT(0) if it is non-positively curved (in the sense of comparison geometry).

Gromov showed that a cube complex is CAT(0) if and only if it is simply connected, and if the link of every vertex is a flag complex (i.e. every complete subgraph of the 1-skeleton are the edges of a simplex in the complex). A cube complex satisfying the flag condition without necessarily being simply connected is said to be nonpositively curved, or NPC. The universal cover of an NPC complex is a CAT(0) cube complex (actually, Ian must consider slightly more general “orbi-NPC complexes”, which can be thought of as locally the quotient of a CAT(0) complex by a finite group acting cellularly, but not freely; we ignore this issue for simplicity).

The edges in a cube complex fall into equivalence classes, where two edges are equivalent if they are on opposite sides of a square in the complex. Dual to an equivalence class is a hyperplane, which can be thought of as a collection of codimension 1 faces in each cube dual to the edges in that cube in the given equivalence class.

Haglund and Wise singled out a particular class of NPC cube complexes, which they call special cube complexes.

Definition: A special cube complex is an NPC cube complex C satisfying the following conditions:

(i) hyperplanes are embedded;

(ii) hyperplanes are 2-sided (this can be arranged by passing to a 2-fold cover if necessary, given (i))

(iii) there are no self-osculating hyperplanes; and

(iv) there is no interosculation.

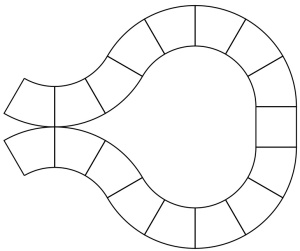
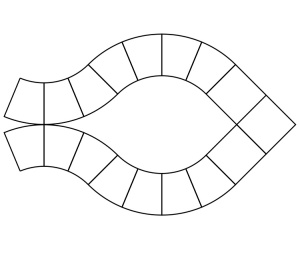
Self-osculation rules out the following kind of picture, where a hyperplane comes back and bounds a “monogon” with itself:

while interosculation rules out the condition that two hyperplanes osculate somewhere and are transverse elsewhere:

Haglund-Wise show (and this is the main reason to introduce the class of special NPC complexes) that the fundamental group of a special NPC cube complex embeds into a right-angled Artin group (RAAG) with one generator for each hyperplane , with the relation that and commute whenever hyperplanes cross, and no other relations. (Artin groups are a kind of “complexification” of Coxeter groups; if one takes a real hyperplane arrangement which are the fixed sets of the generators of a Coxeter group and complexifies it to obtain a complex hyperplane arrangement, and then takes the quotient of the complement of the complex hyperplane arrangement by the (complexified action of the) Coxeter group, the fundamental group of the quotient is an Artin group.) RAAGs are very nice groups, with many very useful properties. For Agol’s purposes, the most important property is that if G is a (word) hyperbolic RAAG, and H is a quasiconvex subgroup (i.e. if we think of G as a metric space via the Cayley graph construction, then every geodesic in G which starts and ends in H stays within a bounded distance of H) then H is subgroup separable. This means that for every g in G but not in H there is some homomorphism from G to a finite group in which the image of g is not contained in the image of H.

With this terminology, the main technical theorem Agol proves is the following:

Theorem(Agol:) Let G be a hyperbolic group acting properly discontinuously and cocompactly on a CAT(0) cube complex X. Then there is a finite index subgroup H of G so that the quotient of X by H is special.

One concludes from Haglund-Wise that if G is a hyperbolic group acting properly discontinuously and cocompactly on a CAT(0) cube complex X, then quasiconvex subgroups of G are separable.

What does this have to do with 3-manifolds? This is where the work of Kahn-Markovic (discussed on this blog a couple of years ago) comes in. Recall that Kahn-Markovic proved the famous Surface Subgroup Conjecture by showing that every closed hyperbolic 3-manifold contains many immersed surfaces S which are very nearly totally geodesic, and whose fundamental group therefore injects into that of M. If one could find a finite cover of M in which one of these surfaces became embedded, one could deduce easily from its geometry (and from Gauss-Bonnet) that the surface was incompressible and boundary incompressible, and therefore one would deduce that M was virtually Haken. Now, the universal cover of the surface certainly embeds in the universal cover of M (in fact, it is very close to a flat hyperbolic plane), but the problem is that different lifts of the surface might intersect each other transversely. These different lifts correspond to elements of the fundamental group of M that are not conjugate into the fundamental group of S. If one knew that the fundamental group of S was separable (in the sense above), one could pass to finite covers in which these “bad” elements failed to lift, one by one, until some finite cover of S became embedded; so if one knew that the fundamental group of M acts properly discontinuously and cocompactly on a CAT(0) cube complex, one could apply the theorem of Agol (above) and prove that M is virtually Haken. But where to find such an action?

The key is that Kahn-Markovic produce not just one immersed surface S, but many such surfaces — so many that one can be found arbitrarily close to any immersed totally geodesic plane on any compact subset. The circle at infinity of the universal cover of such a surface is an almost-round quasicircle in the sphere at infinity of hyperbolic 3-space, and this collection of circles crisscrosses the sphere all over the place. In fact, so many surfaces can be found that we can find one separating any pair of distinct points in the sphere at infinity. This collection of almost-flat planes crashing through hyperbolic 3-space should make one think of a hyperplane arrangement decomposing Euclidean space into cells. The fundamental group of M acts by permuting this cell structure. The idea is that one should think of these (3-dimensional) cells as the “shadows” of higher dimensional cubes — the cubes in the sought-after cube complex on which the fundamental group will act.

(Note: the next two paragraphs are my partial summary of the second talk this morning by Nicolas Bergeron). The idea of building a cube complex from a collection of (suitable) immersed submanifolds goes back to a remarkable construction of Sageev from the early 90’s (also see here). Sageev’s construction starts with a hyperbolic group G and a collection of codimension 1 subgroups . A subgroup H of G is said to be codimension 1 if for some the neighborhood of H in the Cayley graph of G separates the Cayley graph into at least 2 distinct (non cofinite) H-orbits (to say these orbits are not cofinite means that their quotient by H is not compact). In the case in question, G will be the fundamental group of a hyperbolic 3-manifold, and the will be the fundamental groups of lots of Kahn-Markovic surfaces — enough to separate pairs of points at infinity. The collection of universal covers of the surfaces in the universal cover of M will become the hyperplanes of the cube complex. Each surface decomposes into two halfspaces; a 0-cube of the cube complex corresponds to a choice of one halfspace for each surface satisfying the following two properties:

(1) if are two halfspaces, and is one of the chosen halfspaces, then B must also be a chosen halfspace; and

(2) every point in lies in all but finitely many of the chosen halfspaces.

In this correspondence, the halfspaces “corresponding” to a given vertex will be exactly the sides of the associated hyperplanes facing the vertex in the cube complex. A 1-cube of the cube complex corresponds to a pair of 0-cubes which differ in the choice of halfspace associated to exactly one surface; in the cube complex, this is the unique hyperplane crossing the associated edge. It turns out that, having specified the 0 and 1 cubes, there is a unique way to complete the result to be CAT(0).

Sageev showed that G as above acts cocompactly on this cube complex (which is finite dimensional). Bergeron-Wise showed that the fact that the surfaces separate pairs of points at infinity is enough to guarantee that the action is proper, and therefore one deduces that the fundamental group of a hyperbolic 3-manifold M acts properly discontinuously and cocompactly on a CAT(0) cube complex, and (by Agol), is virtually special. So one concludes that the surface subgroups are separable after all, and therefore M is virtually Haken!

None of this even touches on the new ingredients in Ian’s argument, or Wise’s key work on quasiconvex virtual hierarchies and his malnormal quotient theorem; nor does it get to the work of Agol-Manning-Groves which combines with the malnormal quotient theorem to prove a “weak” separability theorem which allows Ian to begin his inductive proof that NPC groups are virtually special. But that’s for the next post (oof!)

(edited March 27: corrected typos, and changed pictures of inter/self osculating complexes to make them more generic)