Roots, Schottky semigroups, and Bandt’s Conjecture

It has been a busy quarter. Since August, I have made 10 trips, to conferences or to give colloquia. On 8 out of the 10 trips, I talked about a recent joint project with Sarah Koch and Alden Walker, on a topic in complex dynamics; our paper is available from the arXiv here. Giving essentially the same talk 8 times (to reasonably large crowds each time) is an interesting experience. The same joke works some times but not others. An explanation that has people nodding their head in one place is met with blank stares in another. A definition passes without comment in one crowd, but leads to a prolonged back-and-forth in another. The nature of the talk (lots of pictures!) meant that I gave a computer talk with slides, so that the overall structure and flow of the talk was quite similar each time; however, I also tried to combine the slides with the occasional use of the blackboard, and some multimedia elements (an animation, an interactive session with a program). I believe my presentation was very similar each time. But my impression of how well the talk went and was received varied tremendously, and I am at a loss to explain exactly why.

In any case, I am officially “retiring” this talk, so for the sake of variety, and while I am still at the point where everything is very coherent and organized in my mind, I will attempt to translate the talk into a blog post.

0. Idle curiosity

This project started with my daydreaming in the bath, some time last March. I let my mind wander, and started to think about some simple piecewise-linear dynamical systems defined on the unit interval, which arise naturally in the theory of Bernoulli convolutions. Some basic questions about these systems seemed easy, and others more subtle. As my mind drifted, I wondered about the complexification of these systems; now the basic questions seemed harder, but it occurred to me that I could write a computer program to investigate them.

With a bit of work (mostly debugging), I had a program running and generating pictures, full of some striking (and completely unexpected!) complexity and beauty. Without giving any more context, here are some samples of the output:

This last picture reminded me a bit of Hokusai’s The Great Wave off Kanagawa. Tereez posted it on her Facebook page, and Amie Wilkinson, in a fit of remarkable creativity, made a fabric print out of it, from which she made a pillow and a dress:

Anyway, out of fascination with the apparent structure and intricacy in these dynamical systems, I pursued them further, soon sharing some ideas and questions with Sarah Koch. Shortly after, Alden Walker came on board, and we have spent a very interesting and rewarding 9 months or so teasing out some of the apparent structure that our computer programs produced, proving some things, conjecturing others, and discovering connections to work of various other people that was done over a period stretching back several decades.

1. Pairs of similarities

We are concerned with dynamical systems which are at first glance of a very simple sort. These dynamical systems consist of semigroups of contracting similarities of the Euclidean plane. Or, identifying the Euclidean plane with the complex numbers, the elements of the semigroup are complex affine maps of the form $x \to \alpha x + \beta$ for complex numbers $\alpha$ , $\beta$ with $|\alpha|<1$ . The number $\alpha$ is the dilation factor of the contraction. Our semigroups are finitely generated; in fact, they are generated by two elements $f$ and $g$ ; and we further insist that these two elements have the same dilation factor. Any contracting similarity of the complex plane has a unique fixed point; if we conjugate by a similarity, we can put the two fixed points of the generator $f$ and $g$ wherever we want. Thus, all such two-generator semigroups are conjugate to a pair of the form

$f:x \to zx+1, \quad g:x \to zx-1$

for some $|z|<1$ . In other words, up to conjugacy, each semigroup is specified by a single complex number $z$ of norm less than 1.

In fact, I have described here not a single semigroup, but a family of semigroups $G(z)$ depending on a complex parameter $z$ . The most natural and fundamental question is: how does the dynamics of the semigroup depend on the parameter $z$ ?

2. Limit set

In the study of a dynamical system, one natural first step is to look for invariant sets; in our context, this means looking for a set $\Lambda$ for which $\Lambda = f\Lambda \cup g\Lambda$ . Arbitrary sets are (in general) too complicated; so we should further look for a closed, nonempty set $\Lambda$ . If we further insist that $\Lambda$ should be compact, then there is only one such $\Lambda$ that will fit the bill, and this is called the limit set of the semigroup. Here are some examples, for six different values of $z$ :

In each case, since $\Lambda = f\Lambda \cup g\Lambda$ , we can color $f\Lambda$ blue and color $g\Lambda$ orange (and let blue win “ties” for points that are in $f\Lambda \cap g\Lambda$ ). Thus, the limit set is made of two scaled, rotated copies of itself, the copies displaced from each other by a translation. The limit set can be disconnected (as in cases 1 and 3 above), or connected but not simply connected (cases 4 and 5) or topologically a disk (case 2) or a dendrite (case 6), or one of many other possibilities.

There are several ways to define $\Lambda$ . One characterization of $\Lambda$ is that is is the closure of the set of fixed points of elements of $G(z)$ . This set is obviously closed; to see that it is invariant, observe that if $p$ is fixed by $u$ , then it is also fixed by $u^n$ for any $n$ , and $vp$ is the limit of the fixed points of $vu^n$ . This shows that $f\Lambda \cup g\Lambda \subset \Lambda$ . To see the other direction, if $p$ is fixed by $u$ which starts with $f$ (say), then $p \in u\Lambda \subset f\Lambda$ , so that $f\Lambda \cup g\Lambda = \Lambda$ .

Another description of $\Lambda$ is algorithmic. Suppose that $D$ is a compact disk in the plane with the property that $fD$ and $gD$ are both contained in $D$ . Then $fD \cup gD \subset D$ , and by induction, if $G_n$ denotes the set of elements of $G(z)$ of (word) length $n$ , we have

$G_nD \subset G_{n-1}D \subset \cdots \subset D$

so that $\Lambda = \cap_n G_nD$ .

A third definition involves infinite words. Suppose $w$ is a right-infinite word in the generators $f,g$ with finite prefixes $w_n$ of each finite length $n$ . If we fix any point $p$ then for any $n<m$ we have $|w_n(p) - w_m(p)| = |z|^n |p - u_{n,m}(p)|$ where $w_m = w_n u_{n,m}$ for some word $u_{n,m}$ of length $m-n$ . If $p \in \Lambda$ then so is $u_{n,m}(p)$ , so that $|p-u_{n,m}(p)|$ is no greater than the diameter of $\Lambda$ , some fixed constant. It follows that $w_n(p)$ is a Cauchy sequence, and independent of the choice of $p$ , so that there is a well-defined map $\pi$ from the set of right-infinite words to $\mathbb{C}$ . We denote the set of right-infinite words by $\partial G$ ; topologically, it is a Cantor set with the product topology, and the map $\pi$ is continuous, and its image is exactly $\Lambda$ .

3. Schottky semigroups

Suppose that $f\Lambda \cap g\Lambda = \emptyset$ . Then this decomposition witnesses that $\Lambda$ is disconnected. Conversely, it turns out that if $f\Lambda \cap g\Lambda$ is nonempty, then $\Lambda$ is connected, and even path-connected.

One way to certify that $f\Lambda \cap g\Lambda = \emptyset$ would be to find some compact disk $D$ so that $fD,gD \subset D$ , and $fD \cap gD=\emptyset$ , for then $\Lambda \subset D$ , and $f\Lambda \subset fD$ , $g\Lambda \subset gD$ so that $f\Lambda \cap g\Lambda = \emptyset$ . In this case by induction we see that $uD \cap vD = \emptyset$ whenever $u,v \in G_n$ are distinct words of length $n$ . Since the diameters of $w_nD$ go to zero uniformly for $w_n$ the prefixes of a right-infinite word $w$ , it follows that in this case, $\Lambda$ is a Cantor set. In this case we call $G(z)$ a Schottky semigroup, by analogy with the (more familiar) Schottky groups familiar from the theory of Kleinian groups. A disk $D$ with the properties above is called a good disk for the semigroup.

In fact, it turns out that $\Lambda$ is disconnected if and only if it admits a good disk, so that this is if and only if $\Lambda$ is a Cantor set, and $G(z)$ is Schottky. One way to see this is to appeal to the following:

Short Hop Lemma. If $\delta$ is the distance from $f\Lambda$ to $g\Lambda$ , then the $\delta/2$ neighborhood $N_{\delta/2}(\Lambda)$ of $\Lambda$ is (path) connected.

This is easily proved by induction. Note that if $\delta>0$ it immediately implies that for such a $\delta$ , the neighborhoods $N_{|z|\delta/2}(f\Lambda)$ and $N_{|z|\delta/2}(f\Lambda)$ are connected and disjoint; so we can define $E$ to be the filled set obtained from $N_{\delta/2}(\Lambda)$ by filling in the holes (if any) to make it simply-connected, and then let $D$ be a disk obtained by enlarging $E$ slightly.

We thus have a fundamental dichotomy: for each $z$ , either $\Lambda$ is path-connected, which happens if and only if $f\Lambda \cap g\Lambda$ is nonempty; or $G(z)$ is Schottky, and $\Lambda$ is a Cantor set. So the natural question is: how does the connectivity of $\Lambda$ depend on $z$ ?

At this point we are starting to ask more substantial questions, and it is proper to begin to discuss some of the history of the subject. The semigroups $G(z)$ discussed above were first studied by Barnsley and Harrington in 1985. They were the first to observe the fundamental dichotomy above, and in order to study it systematically, they introduced the following object in parameter space:

Definition (Barnsley and Harrington, 1985) The “Mandelbrot set” $\mathcal{M}$ for the semigroups $G(z)$ is the set of $z$ with $|z|<1$ for which $\Lambda_z$ is connected (equivalently, for which $G(z)$ is not Schottky).

Describing $\mathcal{M}$ is supposed to suggest an analogy with the Mandelbrot set, i.e. the set of complex numbers $c$ for which the Julia set of the quadratic polynomial $z \to z^2 + c$ is connected. Thus in this “dictionary”, the Julia set of a quadratic polynomial corresponds to the limit set of a semigroup. In the former case, the dynamical system is generated by a single complex endomorphism of degree 2, whereas in our case it is generated by two endomorphisms of degree 1. An intriguing context interpolating between both worlds are the correspondences, studied by Shawn Bullet and Christopher Penrose.

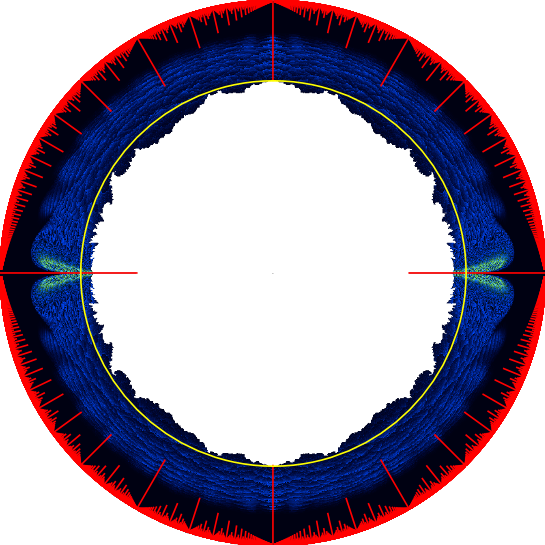
Here is a picture of $\mathcal{M}$ :

Every colored pixel is some $z \in \mathcal{M}$ ; the Schottky $z$ are in white. The color of the pixels is of secondary importance, and concerns the runtime of the algorithm on the input $z$ which produced the picture.

If $G(z)$ and $G(z')$ are both Schottky with good disks $D$ and $D'$ , then the dynamics of $G(z)$ on $D$ is conjugate to the dynamics of $G(z')$ on $D'$ . This can be proved by choosing a homeomorphism from $D - f_zD - g_zD$ to $D' - f_{z'}D' - g_{z'}D'$ which is compatible on the boundaries, extending it over the forward images, and then filling it in over the (Cantor) limit sets. Thus, from a dynamical point of view, there is nothing “interesting” about the Schottky semigroups — they are all the same as each other, more or less.

(Actually, it is worth remarking that $G(z)$ and $G(z')$ will not usually be conjugate on the entire plane. For, they are invertible on the plane, so such a conjugacy would extend to a conjugacy between the groups they generate. But these groups act indiscretely, and will almost never be conjugate).

Note that the Schottky condition is open; thus $\mathcal{M}$ is a closed set.

4. Roots

Up to this point we have introduced a family of dynamical systems parameterized by a single complex number $z$ , associated an interesting compact invariant set $\Lambda_z$ to each parameter $z$ , and made some connections between the topology of $\Lambda_z$ and the dynamics of the semigroup. But there is a special feature of this family of dynamical systems that makes them especially interesting, and that has to do with a direct connection to number theory, via roots.

In a nutshell, for every parameter $z$ , the limit set $\Lambda_z$ has the following concise description:

$\Lambda = \lbrace \text{values of power series with coefficients in } -1,1\rbrace$

This is surprisingly easy to see. We have already shown that points in $\Lambda$ are of the form $\lim_{n \to \infty} w_n(x)$ for any fixed $x$ , and for some sequence of words $w_n$ which are the prefixes of a right-infinite word $w$ . For any word $w_n$ of length $n$ , the map $x \to w_n(x)$ is a contraction with dilation factor $z^n$ , so it is necessarily of the form $x \to z^nx + \beta(w_n,z)$ . How does $\beta(w_n,z)$ depend on $z$ ? I claim it is a polynomial of degree $n-1$ , whose coefficients are $1$ or $-1$ according to whether the successive letters of $w_n$ are $f$ or $g$ . To see this, consider how $f:p(z) \to zp(z)+1$ acts on polynomials $p(z)$ in $z$ . Multiplication by $z$ just shifts the coefficients to the right by one, and then we append $1$ as the constant coefficient (for $g$ in place of $f$ we append $-1$ as the constant coefficients). This proves the claim, and shows that the image of the infinite word $w$ is the value of the power series $\sum_{j=0}^\infty a_jz^j$ where $a_j=1$ if the $j$ th letter of $w$ is $f$ , and $a_j=-1$ otherwise.

But now what is $\mathcal{M}$ ? A point $z$ is in $\mathcal{M}$ if and only if $f\Lambda \cap g\Lambda$ is nonempty. This means that there is an equality of two power series

$a_0 + a_1z + a_2z^2 + \cdots = b_0 + b_1z + b_2z^2 + \cdots$

where the first is in $f\Lambda$ and the second in $g\Lambda$ . Points in $f\Lambda$ are in the image of right-infinite words $w$ which start with $f$ , so these correspond to power series that start with $1$ ; conversely, points in $g\Lambda$ correspond to power series that start with $-1$ . So $a_0=1$ and $b_0=-1$ , and by taking the difference we get an expression

$2 + (a_1-b_1)z + (a_2-b_2)z^2 + \cdots = 0$

Every coefficient of this power series is one of $2,0,-2$ , and all such power series arise this way. Dividing by $2$ , we see that $\mathcal{M}$ is exactly the set of roots of power series each of whose coefficients is equal to one of $1,0,-1$ . Since $\mathcal{M}$ is closed, we obtain the following characterization:

Proposition: $\mathcal{M}$ is equal to the set of roots (of absolute value less than 1) of polynomials with coefficients in $\lbrace -1,0,1\rbrace$ .

The closure of the set of all such roots (including those of absolute value greater than 1) is obtained as the union of $\mathcal{M}$ with its image under inversion in the unit circle (together with the unit circle itself, of course).

This elementary but profound relationship between roots and complex (linear) dynamics has been discovered independently many times. It was discussed in the original paper of Barnsley-Harrington, and (in a very closely related context) in a paper of Odlyzko-Poonen. More recently, similar connections were made by Sam Derbyshire, Dan Christensen and John Baez, and in Bill Thurston’s last paper these and similar sets make an appearance because of their connections to core entropy of Galois conjugates of post-critically finite interval maps on the main “limb” of the (usual) Mandelbrot set.

5. Holes and Interior Points

In their paper, Barnsley-Harrington made many experimental observations, some of which they codified as conjectures or questions, and some which they were able to prove. One intriguing and apparent feature of the picture of $\mathcal{M}$ are the whiskers; i.e. the (totally) real “spikes” which jut into Schottky space. It appear numerically that these whiskers are isolated; i.e. that in some open neighborhood of their endpoints, the intersection with $\mathcal{M}$ is totally real (note that $z \in \mathcal{M} \cap \mathbb{R}$ if and only if $|z|\ge 1/2$ ).

Another observation they made, which is unexpected if one naively expects a very close analogy with the ordinary Mandelbrot set, is that Schottky space is (apparently) disconnected: on zooming in, one finds many (apparent) tiny holes in $\mathcal{M}$ . One such hole is near $latex -0.5931+0.3644 i$:

The limit sets at this parameter look for all the world like a pair of oddly-shaped “gears”, whose teeth interlock so that the two gears are disjoint, but can’t be separated from each other by a rigid motion:

Floating near this “exotic hole” are smaller exotic holes; when we pick a point in one of these smaller holes, and zoom in on the limit set, we discover that the “teeth” on the gears themselves have smaller “teeth”, and now the teeth-on-teeth are interlocked. When we pick a point in yet a smaller hole, we discover the teeth-on-teeth have their own teeth, and these teeth-on-teeth-on-teeth are now interlocked . . . and so on, to the limits of numerical resolution.

The existence of at least one “exotic” hole was rigorously confirmed by Christoph Bandt in 2002, using techniques developed by Thierry Bousch (unpublished, but see his web page) in 1988. Bousch showed by a lovely argument that $\mathcal{M}$ is connected and locally connected (the fact that the ordinary Mandelbrot set is connected is a theorem of Douady and Hubbard; its local connectivity is the most significant outstanding conjecture about its structure), and gave a technique for constructing continuous paths in $\mathcal{M}$ . Bandt adapted Bousch’s techniques, and used them to give a rigorous (numerical) proof of the existence of paths in $\mathcal{M}$ circling apparent holes, thus certifying their existence.

But the apparent self-similar structure of $\mathcal{M}$ (noted by Barnsley-Harrington) strongly suggests that if there is one exotic hole, there should be infinitely many, and perhaps even a combinatorial dynamical systems that organizes them. Bandt found a very suggestive self-similarity for $\mathcal{M}$ at certain points, called landmark points. Giving a precise definition of these points is not straightforward, but they have the interesting property that at such a point, $f\Lambda \cap g\Lambda$ consists of a single point, which implies that the limit set $\Lambda_z$ is a dendrite. Bandt asserted, and Eroglu-Rohde-Solomyak showed, that at such points $\Lambda_z$ is quasisymmetric to the Julia set of some rational map; in fact, one can think of the restrictions of $f$ and $g$ to $\Lambda_z$ as the two inverse branches of a quadratic map with critical point at $f\Lambda \cap g\Lambda$ , and the conjugacy between limit set and Julia set respects this dynamics.

Landmark points are the analog of Misiurewicz points in the ordinary Mandelbrot set. At such a point $c$ , Tan Lei famously proved that the Mandelbrot set and the Julia set associated to $z \to z^2 +c$ are (asymptotically) self-similar. Analogously, Solomyak proved that at a landmark point $z$ , the set $\mathcal{M}$ is asymptotically self-similar to a limit set $\Lambda'$ associated to the three-parameter semigroup $x \to zx-1, x \to zx, x \to zx+1$ . So there is a natural strategy to try to prove the existence of infinitely many holes in $\mathcal{M}$ . Firstly, find a landmark point. Second, find a nearby exotic hole; and thirdly, use self-similarity to show that the images of the hole under the self-similarity spiral down to the landmark point, and are distinct from each other.

This is a good strategy, but to realize it is not straightforward. The problem is that the kind of self-similarity Solomyak proves is too weak: the rescaled copies of $\mathcal{M}$ and $\Lambda'$ converge to each other on compact subsets, but only in the Hausdorff metric. Thus, this self-similarity says nothing whatsoever about the topology of the sets or their convergence; it might be that the apparently distinct holes are connected by asymptotically infinitely thin lines to the main component, and so are not distinct after all.

After some thought it becomes clear that the main obstacle to fleshing out this strategy, or gaining a finer understanding of $\mathcal{M}$ in general, is to understand the structure of the set of interior points. Bandt already recognized this in his paper, and he made the following conjecture:

Conjecture (Bandt): Interior points are dense in $\mathcal{M}$ away from the real axis.

The need to exempt $\mathcal{M} \cap \mathbb{R}$ is already clear from Barnsley-Harrington’s discovery of the whiskers.

6. Two methods to construct interior points

Let me now give two somewhat complementary methods to certify that certain points $z$ are in the interior of $\mathcal{M}$ . The first method is analytic, and is really a sort of counting argument. The second method is topological.

The first method is an argument using Hausdorff dimension. Suppose $z$ is Schottky. What can we say about the Hausdorff dimension of $\Lambda$ ? Suppose this dimension is $d$ . Then since $\Lambda$ is the disjoint union of $f\Lambda$ and $g\Lambda$ , we must have

$H^d(\Lambda) = H^d(f\Lambda) + H^d(g\Lambda)$

where $H^d$ denotes $d$ -dimensional Hausdorff measure. On the other hand, each of $f\Lambda$ and $g\Lambda$ is a copy of $\Lambda$ linearly scaled by $|z|$ , so that $H^d(f\Lambda) = |z|^dH^d(\Lambda)$ . Thus $1=2|z|^d$ so that $d = \log(1/2)/\log(|z|)$ . On the other hand, since $\Lambda$ is a subset of the plane, its Hausdorff dimension is at most 2. It follows that $|z| \le 2^{-1/2}$ , which is approximately $0.707$ . Thus $\mathcal{M}$ contains the entire annulus $\lbrace z: 2^{-1/2} < |z| < 1\rbrace$ , which is thus entirely in the interior. This observation was already made by Bousch in 1988. Solomyak-Xu showed the existence of some interior points with $|z|<2^{-1/2}$ , but their methods are somewhat restricted.

The second method is the topological method of traps. How does a topologist prove that two sets intersect? The most usual way is to use homology (or more naively, separation properties). But if $z$ is not in $\mathcal{M}$ , the sets $f\Lambda$ and $g\Lambda$ are disconnected, and carry no (interesting) homology. The informal idea of traps is to suitably “thicken” these sets so that we can find approximate intersections for topological reasons, and then argue that these approximate intersections can be perturbed to honest intersections.

Suppose $A$ and $B$ are path connected, planar sets. We say that $A$ and $B$ are transverse if we can find four points $a_1,b_1,a_2,b_2$ in the frontier of $A \cup B$ in this cyclic order, where $a_i \in A - B$ and $b_i \in B-A$ , and where each of the four points can be joined to infinity by a ray in the complement of $A \cup B$ :

In this figure, $A$ is red, $B$ is blue, and the four points are in black. Transversality implies that any path in $A$ from $a_1$ to $a_2$ must intersect any path in $B$ from $b_1$ to $b_2$ .

Now, suppose we are at some $z$ which we hope to show is in the interior of $\mathcal{M}$ . Let $\delta$ denote the distance from $f\Lambda$ to $g\Lambda$ ; we want to show $\delta = 0$ . In fact, $\delta$ should really be thought of as a function of $z$ . We choose (e.g. numerically) some $D$ which is an upper bound for $\delta$ in some neighborhood of $z$ . Suppose we can find a pair of words $u,v \in G_n$ so that $u$ starts with $f$ , so that $v$ starts with $g$ , and so that the connected (!) sets $A:=N_{|z|^nD/2}(u\Lambda)$ and $B:=N_{|z|^nD/2}(v\Lambda)$ are transverse in the sense above. There is some path in $N_{|z|^n\delta/2}(u\Lambda)$ joining $a_1$ to $a_2$ , and a path in $N_{|z|^n\delta/2}(v\Lambda)$ joining $b_1$ to $b_2$ , and these paths must cross, and therefore the distance from $u\Lambda$ to $v\Lambda$ is at most $|z|^n\delta$ . But

$\delta = \text{dist}(f\Lambda,g\Lambda) \le \text{dist}(u\Lambda,v\Lambda) \le |z|^n\delta$

so $\delta=0$ and therefore $z \in \mathcal{M}$ . Now, the inequality $\delta < D$ and the transversality of $A$ and $B$ are both open in $z$ , so these properties hold for all $z'$ sufficiently close to $z$ , and therefore all sufficiently close $z'$ are in $\mathcal{M}$ . In other words, we have proved that any $z$ for which there is a trap is an interior point of $\mathcal{M}$ .

OK, we have a criterion to prove that some point is in the interior of $\mathcal{M}$ , but when can we use it? First, observe that if $u,v \in G_n$ , then $u\Lambda$ and $v\Lambda$ differ by a translation, so the two sets $A,B$ as defined above differ by a translation. So we are led to consider the more general problem: for which disks $D$ in the plane is there some $\lambda \in \mathbb{C}$ for which $D$ and $D+\lambda$ cross transversely? The surprising answer turns out to be: for exactly those $D$ which are not convex. That this is a necessary condition is clear. How to see that it is sufficient?

Suppose $D$ is not convex, so that there is some supporting line $\ell$ which intersects $\partial D$ in at least two components (without loss of generality, we can assume $\ell$ is horizontal and lies on “top” of $D$ ). There is some open set $U$ trapped between $D$ and $\ell$ between two components of intersection, so there is some $\lambda$ which moves the rightmost point of the leftmost component into $U$ . Since $\lambda$ moves points “to the right”, the rightmost point of $D+\lambda$ is further to the right than the rightmost point of $D$ :

This is a satisfying answer, but it raises a new question: for which $z$ is $\Lambda$ convex? It turns out that one can directly answer this question: these are exactly the $z$ of the form $re^{i\pi p/q}$ for which $p/q$ is a rational in reduced form, and $r\ge 2^{-1/q}$ . These values of $z$ are plotted in the figure below in red.

The yellow circle has radius $2^{-1/2}$ , so that every red spike — with the exception of the real whiskers — is contained in the annulus that we already know is in the interior of $\mathcal{M}$ for reasons of Hausdorff dimension.

From here the proof of Bandt’s conjecture is almost done. Suppose we are at some point $z \in \mathcal{M}$ which is not real, and has $|z|< 2^{-1/2}$ so that necessarily $\Lambda$ is not convex. There is some $\lambda$ so that $\Lambda$ and $\Lambda + \lambda$ cross transversely. Since $z \in \mathcal{M}$ there are a pair of right-infinite words $u,v$ beginning with $f$ and $g$ respectively, with $\pi(u) = \pi(v)$ at $z$ . Since $\pi(u) - \pi(v)$ is holomorphic and nonconstant, it maps some neighborhood of $z$ onto a neighborhood of 0, so the same is true for $u_n(x) - v_n(x)$ for the prefixes $u_n,v_n$ of length $n$ . But $z^{-n}u_n\Lambda$ and $z^{-n}v_n\Lambda$ look like copies of $\Lambda$ translated relative to each other by $z^{-n}(u_n(x)-v_n(x))$ . If $n$ is big, we can find a nearby $z'$ for which this takes the value $\lambda$ . Since the geometry of $\Lambda_z$ and $\Lambda_{z'}$ is very close if $z'$ and $z$ are close, we obtain a trap centered at $z'$ , so that $z'$ is an interior point arbitrarily close to $z$ . This completes the argument.

7. Renormalization and infinitely many holes

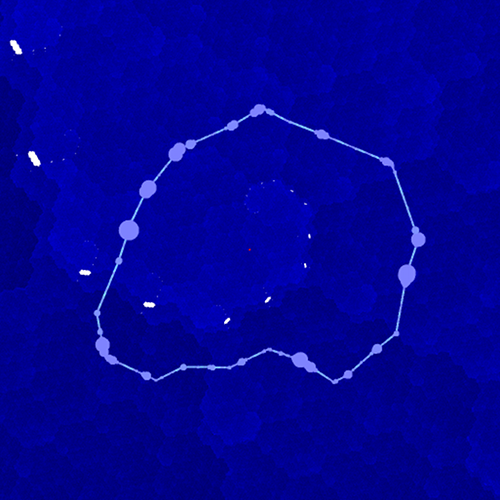
We can use traps to certify exotic holes in $\mathcal{M}$ . First, find the hole numerically, and surround it with a polygonal loop $\gamma$ . If we can find a trap at some point on the loop, it certifies that an open neighborhood of that point is in $\mathcal{M}$ . Finitely many such traps certify that all of $\gamma$ is in $\mathcal{M}$ , and certify the hole. What is not obvious at first is that we can use traps to certify the existence of infinitely many holes.

The self-similarity that Solomyak establishes is closely related to the phenomenon of renormalization in the theory of rational maps (and elsewhere). One of the nice things about traps is that they behave in a predictable way under renormalization. That is, at a landmark point $z$ , if we have an (approximate) self-similarity $\tau$ fixing $z$ , and if some nearby point $w$ is a trap for words $u,v$ , then there are words $u',v'$ obtained in a predictable way from $u,v$ which are a trap for $\tau(w)$ (there are several quantifiers and estimates implicit in this claim; in any case it is “asymptotically true” in the limit near $z$ ). It is therefore possible to produce a loop $\gamma$ in $\mathcal{M}$ surrounding a landmark point which can be covered by (finitely many) traps, and then show that the images of these traps under renormalization persist and certify that the images $\tau^n(\gamma)$ are also in $\mathcal{M}$ , and we get an infinite sequence of concentric annuli which certify that a renormalization sequence of holes are really disjoint from each other.

One very pretty example (taken from our paper) is the following:

The tip of the “spiral” is $z \sim 0.371859+0.519411i$ , a root of $1-2z+2z^2-2z^5+2z^8$ . On the left is a (rescaled) part of the limit set $\Lambda'$ of the three-generator semigroup described above. On the right is part of $\mathcal{M}$ near $z$ ; the resemblance is clear.

This figure shows a loop of renormalizable trap balls, separating some exotic holes from the rest. The forward images of this loop certify the existence of infinitely many holes, limiting to $z$ .

The point $z$ as above is pretty special, and the proof that it is a limit of tiny holes is somewhat ad hoc, being an interesting mixture of theory and numerical certificates. However, we (Sarah, Alden and I) make the following related conjectures. First, we denote by $\partial \mathcal{M}$ the “boundary” of $\mathcal{M}$ ; i.e. the complement of the set of interior points.

Conjecture: Algebraic points in $\partial \mathcal{M}$ are dense in $\partial\mathcal{M}$ .

Conjecture: Every non-real point in $\partial \mathcal{M}$ is a limit of a sequence of holes with diameter going to zero.

8. Multimedia

It’s too late to hear me give a talk on this stuff, but I believe Alden and Sarah have some upcoming talks scheduled. Our preprint is available on the arXiv, and the program schottky with which we produced all the figures and numerical certificates is available from my github page. And in fact the very first talk I gave, back in August, was taped by the Graduate School of Mathematical Sciences at the University of Tokyo, who generously allowed me to post the footage on my youtube channel. So, in glorious technicolor, here it is:

1 Response to Roots, Schottky semigroups, and Bandt’s Conjecture

Vikas Kumar says:

February 18, 2015 at 3:11 am

It is a very unique and very interesting blog on
math………..

	tiktok downloader on Bing’s wild involution
	Groups for which qua… on Big mapping class groups and…
	Anonymous on Stiefel-Whitney cycles as…
	Anonymous on Stiefel-Whitney cycles as…
	Israel Socratus Sado… on Bing’s wild involution