Dipoles and Pixie Dust

The purpose of this blog post is to give a short, constructive, computation-free proof of the following theorem:

Theorem: Every compact subset of the Riemann sphere can be arbitrarily closely approximated (in the Hausdorff metric) by the Julia set of a rational map.

A rational map is just a ratio of (complex) polynomials. Every holomorphic map from the Riemann sphere to itself is of this form. The Julia set of a rational map is the closure of the set of repelling periodic points; it is both forward and backward invariant. The complement of the Julia set is called the Fatou set.

Kathryn Lindsey gave a nice constructive proof that any Jordan curve in the complex plane can be approximated arbitrarily well in the Hausdorff topology by Julia sets of polynomials. Her proof depends on an interpolation result by Curtiss. Kathryn is a postdoc at Chicago, and talked about her proof in our dynamics seminar a few weeks ago. It was a nice proof, and a nice talk, but I wondered if there was an elementary argument that one could see without doing any computation, and today I came up with the following.

The construction depends on the idea of an electromagnetic dipole. This is a pair of charged particles of equal but opposite charge; from far away, the two charges almost cancel, and the particle-pair is effectively neutral. The analog of a dipole for a rational map is a factor of the form $(z-a)/(z-b)$ where $|a-b|$ is small; this is a function which is uniformly close to 1 far from the pair $a$ , $b$ . I like the idea of a dipole, as a kind of “component” of a rational function which modifies it in a localized, predictable way, and wonder if it has further uses.

If $f$ is any rational function, and $p$ is a point in the Fatou set of $f$ , we can build a new function $g_\epsilon$ by multiplying $f$ with a dipole centered at $p$ whose zero-pole pair are $\epsilon$ apart. As $\epsilon \to 0$ , we claim (technical assumption: assuming $f$ has no indifferent fixed points or Herman rings) that the Julia sets of $g_\epsilon$ converge in the Hausdorff topology to a set $\hat{p}$ , which consists of the union of the Julia set of $f$ , together with the point $p$ and its preimages under $f$ . This is easy to see: on the complement of the set $\hat{p}$ , the dynamics of $g_\epsilon$ converges uniformly to that of $f$ . On the other hand, $g_\epsilon$ maps a small neighborhood of $p$ over the complement of at most one point in the Riemann sphere; thus this neighborhood contains some point in the Julia set, and likewise for every point in the preimage of $p$ . This proves the claim.

Now suppose we want to approximate the set $X$ (for convenience, suppose $X$ is disjoint from the unit circle). We can start with $f:z \to z^N$ where $N$ is very large, choose a finite set $Y$ which approximates $X$ in the Hausdorff sense ( $Y$ is a “pixelated” version of $X$ – hence “Pixie dust”), and multiply $f$ by a dipole centered at each point of $Y$ . If $N$ is very big, the Julia set is as close as we like to the union of $Y$ with the unit circle. But after conjugating by a conformal map, the unit circle can be made as small as we like, and moved near any point we like, say some point of $X$ . This completes the proof.

It is interesting that although such rational functions are essentially trivial to write down, drawing their Julia sets is bound to be disappointing. This is because when the zero-pole pair of the dipole are very close, the dipole is numerically indistinguishable from the constant function 1 at the resolution of the pixels in a drawing.

Here are four examples, with $N=2$ , and 80 dipoles, with $\epsilon = 0.2, 0.1, 0.05, 0.02$ . The dipoles spell out a faint pixelated “HI” at the top of each figure, and the prominent circle is (close to) the unit circle.

When I mentioned this construction to Curt McMullen, he alerted me to another preprint by Oleg Ivrii, which gives another, quite different, construction of a polynomial with quasi-circle Julia set which approximates any given Jordan curve (apologies if there are alternate constructions by other people that I have not mentioned).

(Update November 4:) Oleg Ivrii gives yet another (even shorter!) construction of a Julia set approximating any closed set, in the comments below.

(Update November 13:) Merry Xmas!

6 Responses to Dipoles and Pixie Dust

K Hughes says:

November 3, 2014 at 10:22 am

This is a very nice proof. As an analyst, I’m curious, how does the convergence depend on $N$. More precisely, I don’t know any dynamics, so could you please quantify your statement: “If $N$ is very big, the Julia set is as close as we like to the union of $Y$ with the unit circle.”?

Cheers,
K

- Danny Calegari says:
  
  November 3, 2014 at 10:34 am
  
  Dear K –
  
  the order in which to do the approximation is (i) first choose a (big) N; then (ii) take $\epsilon$ small enough so that the Julia set is “predictable” (as a function of N).
  
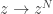  In the more general situation that we start with an arbitrary (generic) f, as $\epsilon$ goes to zero the Julia sets of $g_\epsilon$ converge to $\hat{Y}:=(J_f \cup Y \cup f^{-\circ n}(Y))$ . If we are taking f just to be $z \to z^N$ then the points in 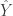$\hat{Y}$ are just the union of Y and the unit circle, and the $N^k$ th roots of points in Y, for all (positive) k. Thus, the absolute value of every such point is the $N^k$ th root of the absolute value of a point in Y; these absolute values go to 1 very quickly with N.
  
Oleg Ivrii says:

November 4, 2014 at 4:29 am

Let me give a similar construction to the one above using dipoles. Given a finite set of points $p_1, p_2, \dots p_k$, one can take the polynomial $P(z) = C (z-p_1)(z-p_2)\dots(z-p_k)$ where $C$ is a sufficiently large constant. It is not hard to see that the Julia set of $P(z)$ is a Cantor set Julia set concentrated near the $p_i$.
I was inspired by the following observation, perhaps due to Thurston: given a finite set of points as before, there exists a Kleinian group whose limit set is concentrated near this set of points: one can take the Schottky group generated by reflections in small circles centered at these points.

Danny Calegari says:

November 4, 2014 at 6:35 am

Oh – very elegant! Thanks for sharing this!

Laura DeMarco says:

November 13, 2014 at 7:26 am

Hi Danny. To me, the strength in Kathryn Lindsey’s construction is not the approximation of the Julia set itself, but that it can be done with a large *filled* Julia set. That is, a large open subset of the interior of given Jordan curve is contained in a bounded Fatou component of the constructed polynomial. Oleg’s construction is probably the easiest way to do this with the Julia set alone. In fact, that same construction allows one to approximate any give probability *measure* on the set, not only the set itself. One can simply choose the roots p_i according to a chosen distribution, and let the degree tend to infinity. I discuss this somewhat in my work about the moduli spaces of rational maps and polynomials, when looking at limits as sequences head out to infinity in these spaces. (And as in Oleg’s comment, my work on this topic was first inspired by some of Thurston’s work, specifically http://arxiv.org/pdf/math/9801088.pdf)

- Danny Calegari says:
  
  November 13, 2014 at 7:57 am
  
  Hi Laura – thanks for your comment.
  
  Sure: I was certainly thinking of this construction in terms of limits of rational maps; modifying a rational map by multiplying by an “infinitesimal” (if you like, a “formal”) dipole at a point x produces a new rational map defined on a “cactus” obtained by attaching a “balloon” (i.e. a ${\bf CP}^1$ ) at x and its preimages by f, then attaching further 2nd order balloons to these 1st order balloons in the preimages of the first order balloons, etc. in an infinite tree; this is a sort of “algebraic limit” as the dipole size goes to zero, whose “geometric limit” is just f.

	tiktok downloader on Bing’s wild involution
	Groups for which qua… on Big mapping class groups and…
	Anonymous on Stiefel-Whitney cycles as…
	Anonymous on Stiefel-Whitney cycles as…
	Israel Socratus Sado… on Bing’s wild involution